3D Animation Workshop: Lesson 36: Softimage--From Splines to NURBS | 2

Lesson 36 - Softimage--From Splines to NURBS - Part 3

NURBS stands for Non-Uniform Rational B-Spline. We'll put aside the mathematical significance of this, and focus on the practical. (By the way, although it sounds like a plural, there's no such thing as a NURB, so people often speak of a NURBS curve even though it's redundant.) NURBS curves are the most general form of spline and actually include all the lesser forms within them. Thus we can make any shape of spline whatever with NURBS tools.

NURBS are B-Splines. Just as in the B-Spline example we last saw, the control points do not interpolate the curve. But NURBS provide some big advantages over regular B-Splines.

B-Splines can be difficult to edit because the control points must be moved significant distances to appreciably change the shape of the curve. Notice the effect of moving the central control point in the next two images.

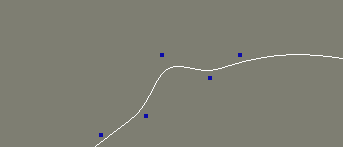
This may not seem like big deal in this simple example, but on complex models covered with control points, moving points large distances can make the model hard to read and edit. With NURBS, we can move control points just as with regular B-Splines. But we can also change the "weight" of the points, affecting their gravitational impact on the curve. Thus a curve can be edited without moving the points at all. Here's the same B-Spline converted to a NURBS curve. Notice how, by changing the weight of the middle point, we can edit the curve without moving the point.

Note also how increasing the weight gives a distinct pointedness to the curvature. Between moving control points and adjusting their weight, NURBS provide a much more flexible tool than regular B-Splines.

Another very important aspect of NURBS curves is the freedom with which they can be cut. A regular B-Spline can only be cut at its "knots," the points along the curve that divide it into segments. Since the control points of a B-Spline do not rest on the curve, it can be hard to even tell where the knots are. For example, I tried to cut the following B-Spline by placing my cursor on the curve at a spot directly above the middle control point. But the cut occurred somewhat to the left, where the knot was located.

With NURBS, we don't need to know where the knots are because we can cut just like we would cut a piece of string, at any spot we pick along the length of the curve.

This short discussion hardly covers the full scope of advantages of NURBS over other splines for modeling, but it's enough to get us started. Next time, we'll look at surfaces made of NURBS curves.

To Return to Parts 1 and 2, Use Arrow Buttons

Previous Lesson / Table of Contents / Next Lesson
Created: March 15, 1998
Revised: March 15, 1998

URL: https://webreference.com/3d/lesson36/part3.html